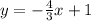We have the following:
The equation in slope and y-intercept form is as follows

where m is the slope and b is the y-intercept.
we can calculate the slope of the perpendicular line with the following formula
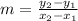
replacing:
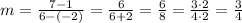
The slope is 3/4 .
When two lines are perpendicular, the slopes are opposite, therefore we can calculate the other slope like this
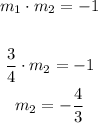
The slope is -4/3, for b, x = - 6 and y = 9, replacing in the equation of the beginning
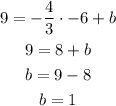
The equation is: