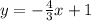Question

Write the equation of a line that passes through the point (-6,9) and is perpendicular to a line that passes through the points (-2, 1) and (6, 7).

Answer 1

We have the following:

The equation in slope and y-intercept form is as follows

`y=mx+b`

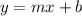
where m is the slope and b is the y-intercept.

we can calculate the slope of the perpendicular line with the following formula

`m=(y_2-y_1)/(x_2-x_1)_{}`

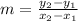
replacing:

`m=(7-1)/(6-(-2))=(6)/(6+2)=(6)/(8)=(3\cdot2)/(4\cdot2)=(3)/(4)`

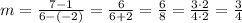
The slope is 3/4 .

When two lines are perpendicular, the slopes are opposite, therefore we can calculate the other slope like this

`\begin{gathered} m_1\cdot m_2=-1 \\ \\ (3)/(4)\cdot m_2=-1 \\ m_2=-(4)/(3) \end{gathered}`

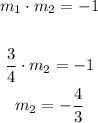
The slope is -4/3, for b, x = - 6 and y = 9, replacing in the equation of the beginning

`\begin{gathered} 9=-(4)/(3)\cdot-6+b \\ 9=8+b \\ b=9-8 \\ b=1 \end{gathered}`

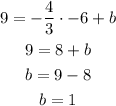
The equation is:

`y=-(4)/(3)x+1`