Question

A 0.75 kg toy is attached to the end of a 1.2m very light string. The toy is whirled in a horizontal circular path on a frictionless tabletop. The maximum tension that the string can withstand without breaking is 450N. What is the maximum speed the toy can have without breaking the string?

Answer 1

Approximately
`26.8\; {\rm m\cdot s^(-1)}`.

Step-by-step explanation:

When an object of mass
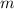`m` travels around a circle of radius
`r` with a (tangential) speed of
`v`, the (centripetal) net force on this object would be
`F_\text{net} = (m\, v^(2) / r)`.

In this question, forces on this toy are:

• Weight.
• Normal force from the tabletop.
• Tension from the string.

It is implied that the table top is horizontal. Hence, weight and normal force on the toy would balance each other. The tension in the string would be equal to the net force on the toy.

Let
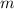`m` denote the mass of the toy, let
`v` denote the linear speed of the toy, and let
`r` denote the radius of the circle. The tension in the string would be equal to the net force
`F_\text{net}` on the toy,
`(m\, v^(2) / r)`.

When the tension in the string is at the maximum value,
`F = 450\; {\rm N}`. Rearrange this equation to find velocity
`v`:

`\begin{aligned}(m\, v^(2))/(r) = F_{\text{net}} \end{aligned}`.

`\begin{aligned}v &= \sqrt{\frac{F_{\text{net}}\, r}{m}} \\ &= \sqrt{((450)\, (1.2))/((0.75))}\; {\rm N} \\ &\approx 26.8\; {\rm N}\end{aligned}`.