Question

Use a series to estimate the following​ integral's value with an error of magnitude less than 10^-5

∫0 0.3 sinx^2dx

Answer 1

`\displaystyle \int\limits^(0.3)_0 {\sin(x^2)} \, dx\approx9*10^(-3)\approx0.009`

Explanation:

`\displaystyle \sin(x)=\sum_(n=0)^\infty(-1)^n(x^(2n+1))/((2n+1)!)=x-(x^3)/(3!)+(x^5)/(5!)-(x^7)/(7!)+...\\\\\\\sin(x^2)=\sum_(n=0)^\infty(-1)^n(x^(2(2n+1)))/((2n+1)!)=x^2-(x^6)/(3!)+(x^(10))/(5!)-(x^(14))/(7!)+...`

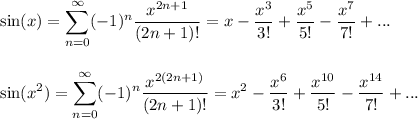
Given our series representation, we can represent the integral value:

`\displaystyle \int\limits^(0.3)_0 {\sin(x^2)} \, dx=\int\limits^(0.3)_0 \biggr[x^2-(x^6)/(6)+(x^(10))/(120)-(x^(14))/(5040)+...\biggr] \, dx\\\\\\=\biggr[(x^3)/(3)-(x^7)/(42)+(x^(11))/(1320)-(x^(15))/(75600)+...\biggr]_0^(0.3)\\\\\\=((0.3)^3)/(3)-((0.3)^7)/(42)+((0.3)^(11))/(1320)-((0.3)^(15))/(75600)+...`

For an error of magnitude less than 10⁻⁵, we would need to consider terms only less than
`\displaystyle ((0.3)^7)/(42)\approx5.207*10^(-6)` as the preceding (and also the first) term
`\displaystyle ((0.3)^3)/(6)=9*10^(-3)` is greater than 10⁻⁵, so the first term should give the required accuracy.

Hence,
`\displaystyle \int\limits^(0.3)_0 {\sin(x^2)} \, dx\approx9*10^(-3)\approx0.009` with an error of magnitude less than 10⁻⁵

Note that the actual value of the integral is
`\displaystyle \int\limits^(0.3)_0 {\sin(x^2)} \, dx=0.00899479419898...` which is very close to our estimate with our error of magnitude being less than 10⁻⁵ or 0.00001