Question

2. Methyl dichloroacetate (Cl2CHCO2CH3) decays into methanol (CH3OH) and dichloroacetic acid (Cl2CHCO2H) on reaction with water. Given a rate constant of 2.7 x 10-4/sec and an initial concentration of 1-ppm methyl dichloroacetate in the water, how much methanol will be present in the water after 30 min

Answer 1

The half-life of the reaction is 4.3 x
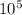`10^5` seconds and the concentration of ethyl chloride after 4 half-lives is 0.0048 M.

Step-by-step explanation:

The decomposition of ethyl chloride into ethylene and HCl is a first-order reaction with a rate constant of 1.6 × 10-6
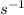`s^{-1`. To find the half-life of the reaction, we can use the formula:

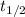`t_(1/2)` = ln(2) / k

Substituting the given value of k, we get:

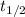`t_(1/2)` = ln(2) / 1.6 × 10-6 s-1 = 4.3 x 105 seconds.

To find the concentration of ethyl chloride after 4 half-lives, we can use the formula:

final concentration = initial concentration ×
`(1/2)^4`

Substituting the given initial concentration, we get:

final concentration = 0.077 M ×
`(1/2)^4` = 0.077 M × 0.0625 = 0.0048 M.

Answer 2

2.69 * 10^-6 Mol/L

Step-by-step explanation:

The equation of the reaction is;

Cl2CHCO2CH3 -------------------> Cl2CHCO2H + CH3OH

To convert from ppm concentration to Mol/L, we have

M = ppm/MM * 1000

Where;

M = mol/l

MM= Molar mass

M = 1/142.97 g/mol * 1000 =

M= 6.99 * 10^-6 Mol/L

For first order reaction;

ln[A] = ln[A]o -kt

Given that

[A]o = 6.99 * 10^-6 Mol/L

[A]=??

k= 2.7 x 10-4/sec

t= 30 mins * 60 = 1800 s

ln[A] = ln[6.99 * 10^-6] - (2.7 x 10-4 * 1800)

ln[A] = -11.87 - 0.486

ln[A] = -12.356

[A] = e^(-12.356)

[A] = 4.3 * 10^-6 Mol/L

Concentration of methanol present after 30 mins= 6.99 * 10^-6 - 4.3 * 10^-6 = 2.69 * 10^-6 Mol/L