Answer:
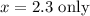
Explanation:
We are given the second derivative:
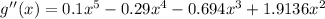
And we want to find the values for -3 < x < 4 in which the graph of g has a point of inflection where the concavity changes from concave up to down.
First, recall that inflection points occur whenever g''(x) = 0 or is undefined.
And that:
- g is concave up for an interval if g''(x) > 0 for that interval.
- g is concave down for an interval if g''(x) < 0 for that interval.
Graphing the function (please refer below for the graph), we can see that g''(x) has an inflection point at x = -2.6, 0, 2.3, and 3.2.
If g''(x) changes from concave up to concave down, the values before and after that inflection point must be positive and then negative.
We can see that g''(x) is only positive for the values before the inflection points at x = 0 and x = 2.3.
However, for values after the inflection points, only x = 2.3 becomes negative.
Therefore, since at x = 2.3, the graph changes from positive to negative, this is where the graph of g changes from concave up to concave down.
Notes:
For the point x = 0, the graph stayed positive both before and after x = 0.
Therefore, g does not have an inflection point at x = 0.