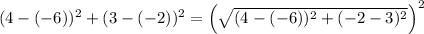Question

I need help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answer 1

jjj

Explanation:

Answer 2

`\textsf{D)} \quad (4 - (-6))^2+(3 - (-2))^2=\left(√((4-(-6))^2+(-2-3)^2)\right)^2`

Explanation:

To find the length of p, subtract the x-coordinate of vertex Q from the x-coordinate of vertex R:

`\implies p=x_R-x_Q`

`\implies p = 4 - (-6)`

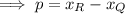
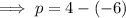
To find the length of q, subtract the y-coordinate of vertex P from the y-coordinate of vertex R:

`\implies q = y_R-y_P`

`\implies q =3 - (-2)`

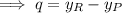
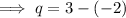
To find the length of r, use the distance formula, where (x₁, y₁) = Q and (x₂, y₂) = P.

`\boxed{\begin{minipage}{7.4 cm}\underline{Distance between two points}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the two points.\\\end{minipage}}`

`\implies r=√((x_P-x_Q)^2+(y_P-y_Q)^2)`

`\implies r=√((4-(-6))^2+(-2-3)^2)`

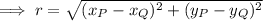
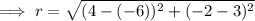
Therefore, the equation that could be used to show p² + q² = r² is:

`(4 - (-6))^2+(3 - (-2))^2=\left(√((4-(-6))^2+(-2-3)^2)\right)^2`