Question

In Parallelogram EFGH, diagonals HF and EG intersect at point D. Give HD = x² – 34 and

DF = x² - 4x. What is HF? Show your work and it would probably help to draw a picture.

Answer 1

HF = 76.5

Explanation:

The diagonals of a parallelogram bisect each other (divide into two equal parts). Therefore, point D is the midpoint of diagonal HF, and so HD = DF.

Find the value of x by equating the expressions for HD and DF and solving for x:

`\implies \sf HD = DF`

`\implies x^2 - 34 = x^2 - 4x`

`\implies -34=-4x`

`\implies 4x=34`

`\implies x=8.5`

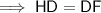
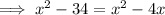
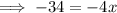
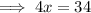
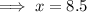
To find the length of HF, substitute the found value of x into the sum of the expressions of HD and DF:

`\implies \sf HF=HD+DF`

`\implies \textsf{HF}=x^2-34+x^2-4x`

`\implies \textsf{HF}=2x^2-4x-34`

`\implies \textsf{HF}=2(8.5)^2-4(8.5)-34`

`\implies \textsf{HF}=76.5`

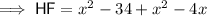
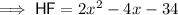
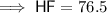
Therefore, the length of HF is 76.5 units.