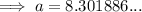Question

Please help math .........

Answer 1

a = 8.3 (1 d.p.)

Explanation:

What are upper and lower bounds?

The maximum and minimum values that a number could have been before it was rounded.

When rounding numbers, check the digit to the right of the one you're rounding to:

• If it is 0, 1, 2, 3 or 4 round down
• If it is 5, 6, 7, 8 or 9 round up

Calculate the upper and lower bounds for p, q and t.

Given p = 8.4:

• The smallest number that will round up to give 8.4 is 8.35, so this is the lower bound.
• The largest number that will round down to give 8.4 is 8.44999… so we say that 8.45 is the upper bound.
• We use ≤ for the lower bound as 8.35 would round up to 8.4, but we have to use < for the upper bound as 8.45 would round up to 8.5, not down to 8.4.

`\begin{array}c\cline{1-3}\vphantom{\frac12} \sf Value & \sf Lower\;bound & \sf Upper\;bound\\\cline{1-3}\vphantom{\frac12} p=8.4 & 8.35 \leq x & x < 8.45\\\cline{1-3}\vphantom{\frac12} q=6.3 & 6.25\leq x & x < 6.35\\\cline{1-3}\vphantom{\frac12} t = 0.27 & 0.265\leq x & x < 0.275\\\cline{1-3}\end{aligned}`

The upper bound for the value of a will be when (p - q) is the greatest value it can be and t is the smallest value it can be.

The upper bound of (p - q) will be when p is at its greatest value and q is at its smallest value.

`\begin{aligned}\implies p-q&=8.44999...-6.25\\& = 2.19999...\end{aligned}`

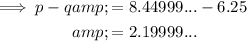
Therefore, the maximum value of (p - q) is 2.19999.....

Therefore the maximum value of a is:

`\implies a=(2.19999...)/(0.265)`

`\implies a=8.301886...`

`\implies a=8.3\; \sf (1 \; d.p.)`