Question

PLEAE HELP ILL GIVE A LOT OF POIINTS

Answer 1

Angle of minor arc

• 360-282=78°

Area

• ∅/360πr²
• 78/360(π(12)²)
• 0.216×3.14×144
• 156π/5 sq in

Answer 2

`\textsf{C)} \quad (156\pi)/(5)\; \sf sq.\;inches`

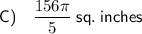
Explanation:

To calculate the area of the colored sector of the circle with radius 12 inches, use the area of a sector formula.

`\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\left((\theta)/(360^(\circ))\right) \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}`

From inspection of the given diagram, the measure of the central angle of the major arc is 282°.

Angles around a point sum to 360°. Therefore, the central angle of the colored sector is:

`\implies 360^(\circ)-282^(\circ)=78^(\circ)`

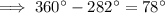
Substitute θ = 78° and r = 12 into the area of a sector formula and solve for A:

`\implies A=\left((78^(\circ))/(360^(\circ))\right) \pi (12)^2`

`\implies A=\left((13)/(60)\right) \pi (144)`

`\implies A=\left((1872)/(60)\right) \pi`

`\implies A=(156\pi)/(5)\; \sf sq.\;inches`

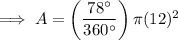
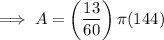
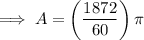
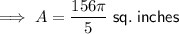
Therefore, the area of the colored sector is:

`(156\pi)/(5)\; \sf sq.\;inches`