Question

Factoring a quadratic with leading coefficient greater than 1: Problem type 1How would you solve this?

Answer 1

We have the trinomial factored as;

`2z^2+19z-21\text{ = (2z+21)(z-1)}`

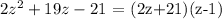
Here, we want to factorize the given quadratic equation

To do this, we will have to rewrite the trinomial

To rewrite, we need to change the middle term to a sum

We need to find two entities of the term z, which when added, will give +19z and when multiplied, they have a product that is equal to (product of the first and the last term);

`2z^2\text{ }*(-21)=-42z^2`

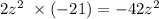
These terms are -2z and 21z

Rewriting the polynomial, we have;

`\begin{gathered} 2z^2-2z+21z-21 \\ =\text{ 2z(z-1) + 21(z-1)} \\ =\text{ (2z+21)(z-1)} \end{gathered}`

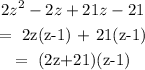
To get the proper factors, the first thing we have to do is multiply the first and last terms

the product is -42z^2

Now, we know that the factors will include z, so we need not bother about that

We list out the factors of -42 (consider the negative and positive numbers since the factor itself is negative)

We have these factors as;

1, -1 , 2 , -2 , 3 , -3 , 6, -6 , 7 , -7 , 14 , -14 , 21, -21 and 42, -42

Now, which of these two can we add that will give +19?

As we can see; -2 and +21 fits this situation perfectly

All we need to do is to add the z after them

Thus, we simply will have -2z and 21z