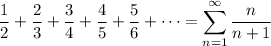Question

Write the sigma notation 1/2 + 2/3 + 3/4 + 4/5 +5/6

I need help with this question! This is AP Calculus.

Answer 1

The n-th term of this sum would be n/(n + 1) - the denominator of each terms is 1 greater than the numerator. In sigma notation, we can write

`\displaystyle \frac12 + \frac23 + \frac34 + \frac45 + \frac56 = \sum_(n=1)^5 (n)/(n+1)`

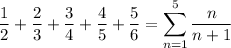
since the first term has numerator 1 and the last term has numerator 5.

If the sum is infinite, we would instead write

`\displaystyle \frac12 + \frac23 + \frac34 + \frac45 + \frac56 + \cdots = \sum_(n=1)^\infty (n)/(n+1)`