Question

Suppose an angle measuring "1 Dip" subtends 1/12th of the circumference of any circle centered at its vertex.Angle A has a measure of 177 degrees. What is the measure of Angle A in Dips? ____Dips   Angle B has a measure of 8 Dips. What is the measure of Angle B in degrees? ______degrees

Answer 1

Answers:

Angle A = 5.9 Dips

Angle B = 240 degrees

Step-by-step explanation:

First, we will calculate how many degrees are equivalent to 1/12th of the circumference, so:

`360\text{ degre}es*(1)/(12)=(360)/(12)=30\text{ degr}ees\text{ }`

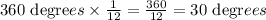
Because a circumference has 360 degrees.

Now, 1 dip subtends 1/12th of the circumference, so 1 Dip has a measure of 30 degrees. Therefore, 177 degrees are equivalent to:

`177\text{ degre}es\text{ }*\frac{1\text{ Dip}}{30\text{ degr}ees}=5.9\text{ Dips}`

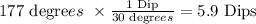
In the same way, 8 dips are equivalent to:

`8\text{ Dips }*\frac{30\text{ degrees}}{1\text{ Dip}}=240\text{ degrees}`

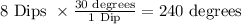
So, the answers are:

Angle A = 5.9 Dips

Angle B = 240 degrees