ANSWER

Step-by-step explanation
To find the surface area of the triangular pyramid given, apply the formula:
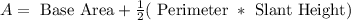
First, we have to find the slant height of the pyramid by applying Pythagoras theorem:
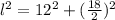
where l represents the slant height.
Solve for l in the equation above:

Now, find the surface area of the pyramid:

That is the answer.