y is the number of minutes spent exercising
x is the number of minutes spent wathcing TV
Linear relationship:
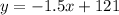
In the equation above:
* The -1.5 represents the rate of change; it represents the change of y for each x.
* The 121 represents the initial value of y, or the value of y when x is 0
Then, for the given statements the next two are true:
- For each additional minute spent whatching TV, the number of minutes spent exercising decreases by 1.5
- If a student watches no TV (x=0) the student will exercise for 121 minutes
Solve y in terms of x to determine if the other two statements are true:
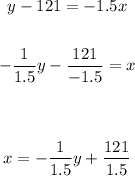
Then, for each additional minute spent exercising, the number of minutes spent watching TV decreases by 1/1.5 (approximately 0.66)
if a student exercises for more than 80 minutes:

Then, if the student exercises for more than 80 minutes, the time watching TV will decrease but it will not be 0 until the time exercising is
Answer:
1. True
2. False
3. False
4. True