Question

Estimate the population in the year 2040

Answer 1

well, in 2007 it was 12000, so initially that's what it was, and in 2019 it went to 23000, so that's 12 years later, and in 2040, that'll be 33 years later.

`\qquad \textit{Amount for Exponential Growth} \\\\ A=P(1 + r)^t\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 23000\\ P=\textit{initial amount}\dotfill &12000\\ r=rate\to r\%\to (r)/(100)\\ t=years\dotfill &12\\ \end{cases} \\\\\\ 23000 = 12000(1 + (r)/(100))^(12)\implies \cfrac{23000}{12000} =\left(1+ \cfrac{r}{100} \right)^(12) \\\\\\ \cfrac{23}{12}=\left(\cfrac{100+r}{100} \right)^(12)\implies \sqrt[12]{\cfrac{23}{12}}=\cfrac{100+r}{100}`

`100\sqrt[12]{\cfrac{23}{12}}=100+r\implies 100\sqrt[12]{\cfrac{23}{12}}-100=r\implies \boxed{5.57\approx r} \\\\[-0.35em] ~\dotfill\\\\ \qquad \textit{Amount for Exponential Growth} \\\\ A=P(1 + r)^t\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{initial amount}\dotfill &12000\\ r=rate\to 5.57\%\to (5.57)/(100)\dotfill &0.0557\\ t=years\dotfill &\stackrel{year~2040 }{33}\\ \end{cases} \\\\\\ A \approx 12000(1 + 0.0557)^(33) \implies \boxed{A \approx 71782}`

Answer 2

Population in the year 2040 is 71,809.91

It seems that the result I got is a complex number, which shouldn't be the case for a population growth problem. This indicates that there may have been an issue with the calculation. Typically, we would expect a real, positive number for a population value.

Let's correct this by using the correct exponential growth formula and recalculate the population estimate for the year 2040. The correct approach is to use the formula:

`\[ P(t) = P_0 * e^(rt) \]`

where:

-
`\( P(t) \) is the population at year \( t \),`

-
`\( P_0 \) is the initial population,`

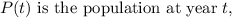
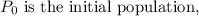
- r is the growth rate,

- t is the time in years since the start of observation.

First, we need to determine the growth rate r based on the population values given for 2007 and 2019. Then we can use this growth rate to estimate the population in 2040. I'll go ahead and do these calculations correctly.

The continuous growth rate r for the population is approximately 0.0542 per year.

Using this growth rate, the estimated population of the town in the year 2040 would be approximately 71,809.91 people.

Here's the step-by-step calculation:

1. We use the given population figures to calculate the growth rate \( r \) with the formula:

`\[ r = (\ln((P_t)/(P_0)))/(t) \]`

where:

-
`\( P_0 = 12000 \) (population in 2007),`

-
`\( P_t = 23000 \) (population in 2019),`

-
`\( t = 12 \) years (from 2007 to 2019).`

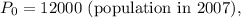
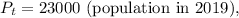
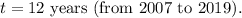
2. After calculating the growth rate, we estimate the population for the year 2040 using the formula:

`\[ P(2040) = P_0 * e^(r * t) \]`

where:

- t = 33 years (from 2007 to 2040).

This results in an estimated population of approximately 71,809.91 for the year 2040.