F(x) = -x² + 5 and g(x) = -2x+2, find all values of x for which f(x) = g(x).

Question

asked Nov 17, 2024 151k views

2 Answers

HowDoIDoComputer · Answer 1 · 2024-11-22T08:17:11+0000

Answer:

The values of x for which f(x) = g(x) are:

Explanation:

To find all the values of x for which f(x) = g(x), equate the given functions:

$\implies f(x)=g(x)$

$\implies -x^2+5=-2x+2$

Rearrange the equation so that it is in the quadratic form ax²+bx+c=0:

$\implies -x^2+5+2x-2=0$

$\implies -x^2+2x+3=0$

Divide both sides by -1:

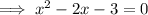
$\implies x^2-2x-3=0$

Factor the quadratic equation:

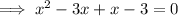
$\implies x^2-3x+x-3=0$

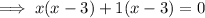
$\implies x(x-3)+1(x-3)=0$

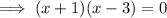
$\implies (x+1)(x-3)=0$

To solve for x, apply the zero-product property:

$(x+1)=0 \implies x=-1$

$(x-3)=0 \implies x=3$

Therefore, the values of x for which f(x) = g(x) are:

We can check the solutions by substituting each found value of x into the functions.

f(-1)=-(-1)^2+5=4

g(-1)=-2(-1)+2=4

f(3)=-(3)^2+5=-4

g(3)=-2(3)+2=-4

As f(-1) = g(-1) and f(3) = g(3), this proves that the values of x for which f(x) = g(x) are x = -1 or x = 3.