Question

Miguel was selling apples, plums, and peaches at the local farmer’s marker. He sold 18 more

pounds of apples than pounds of plums. He sold 9 pounds less of peaches than pounds of
plums. He sold a total of 69 pounds of fruit. How many pounds of each fruit did he sell?

Answer 1

He sold 32 pounds of apples, 14 pounds of plums and 23 pounds of peaches.

Explanation:

Let:

x = Mass of Apples (pounds)

y = Mass of plums (pounds)

z = Mass of peaches (pounds)

He sold 18 more pounds of apple than pounds of plums:
`x = 18 + y`

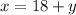
He sold 9 less pounds of peaches than pounds of plums:
`z - 9 = y`

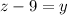
He sold a total of 69 pounds of fruit:
`x + y + z = 69`

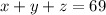
We have 3 unknown variables, therefore a system of 3 linear simultaneous equations:

`x = 18 + y` ——- (equation i)

`z - 9 = y`

∴
`z = 9 + y` ——— (equation ii)

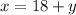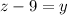
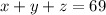`x + y + z = 69` ——- (equation iii)
The above linear simultaneous equations can be solved by Substitution Method:

Substitute (equation i) and (equation ii) into (equation iii) to solve for y. Expand the parenthesis and bring all the like terms together. y has to be made the subject of the equation:

`(18 + y) + y + (y + 9) = 69`

=
`18 + y + y + y + 9 = 69`

=
`y + y + y = 69 - 18 - 9`

=
`3y = 42`

=
`y = (42)/(3)`

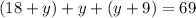
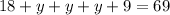
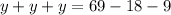
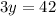
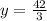
∴ y = Mass of plums = 14 pounds

Substitute the calculated value of y into the other two equations to solve for x and for z:

`x = 18 + (14)`

∴ x = Mass of apples = 32 pounds

`z = 9 + (14)`

∴z = Mass of peaches = 23 pounds