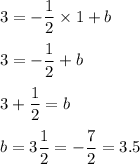Question

Find the equation of the line that passes through (1,3) and is perpendicular to

y=2x-1.
Leave your answer in the form ax+by=c
Where a, b and c are integers.

Answer 1

Equation of perpendicular line:

`\boxed{\quad y=-(1)/(2)x+(7)/(2)\quad }`

Explanation:

Generalized lope-intercept form of a line is y = mx + b [1]

where

m = slope

b = y-intercept

Equation of the given line is y = 2x - 1 [2]

We are asked to find the equation of the line perpendicular to this and also passes through (1, 3)

• Comparing
  `y = 2x + 1` with
  `y = mx+ b` we see that for this line the s
• A line perpendicular to this line will have a slope which is the negative of the reciprocal of this line. The product of the slopes of such two lines will always be - 1
  
• Reciprocal of
  `\mbox{\larg \displaystyle 2 = \displaystyle (1)/(2)}`
  Negative of
  `(1)/(2)` =
  `-(1)/(2)` and this is the slope of the perpendicular line
  The products of the slopes ⇒
  `2 * -1/2 = - 1`
  
• Therefore the equation of the perpendicular line is of the form
  
  `y = -(1)/(2)x + b`
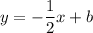
  where b is the y-intercept of this line
  
• Since it passes through the point (1, 3), x= 1 and y = 3 is a solution point on this line
  
• Plugging y = 3, x = 1
  
  
  `3 = -(1)/(2) * 1 + b\\\\3 = -(1)/(2) + b\\\\3 + (1)/(2)= b\\\\b = 3 (1)/(2)= -(7)/(2)= 3.5`