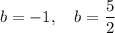Question

The coefficient of x² in the expansion of (2-x)(3 + bx)³ is 45. Find possible values of the

constant b.

Answer 1

The possible values of the constant b are:

`b = -1, \quad b = (5)/(2)`

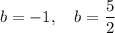
Explanation:

The coefficient of x² in the expansion of (2 - x)(3 + bx)³ can be found by expanding the brackets.

Expand the cubed part by using the (a + b)³ formula:

(a + b)³ = a³ + 3a²b + 3ab² + b³

Therefore:

`\begin{aligned}(3 + bx)^3 &= (3)^3 + 3(3)^2(bx) + 3(3)(bx)^2 + (bx)^3\\&= 27 + 27bx + 9b^2x^2 + b^3x^3\end{aligned}`

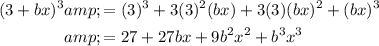
So:

`(2-x)(3 + bx)^3 = (2-x)(27 + 27bx + 9b^2x^2 + b^3x^3)`

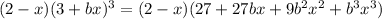
To find the coefficient of the term in x², multiply the constant in the first parentheses by the coefficient of the term in x² in the second parentheses and add this to the product of the coefficient of the term in x in the first parentheses and the coefficient of the term in x in the second parentheses:

`(\bold{2}-x)(27 + 27bx + \bold{9b^2}x^2 + b^3x^3)\\\phantom{.}\underbrace{\uparrow \qquad \qquad\qquad\qquad\;\uparrow}\\ \phantom{wlwww}\text{multiply}`

`(2-x)(27 + \bold{27b}x + 9b^2x^2 + b^3x^3)\\\phantom{bbb..}\underbrace{\uparrow \qquad \quad\;\uparrow}\\ \phantom{ww.w}\text{multiply}`

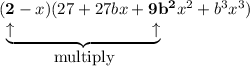
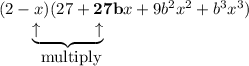
Therefore, the expression for the coefficient of x² is:

`2 \cdot 9b^2 + (-1) \cdot 27b`

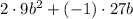
Since the coefficient of x² in the expansion is 45, set the expression to 45 and solve for b:

`\begin{aligned}2 \cdot 9b^2+(-1) \cdot 27b&=45\\18b^2-27b&=45\\18b^2-27b-45&=0\\9(2b^2-3b-5)&=0\\2b^2-3b-5&=0\\2b^2-5b+2b-5&=0\\b(2b-5)+1(2b-5)&=0\\(b+1)(2b-5)&=0\\\\ \implies b+1&=0 \implies b=-1\\ \implies 2b-5&=0 \implies b=(5)/(2)\end{aligned}`

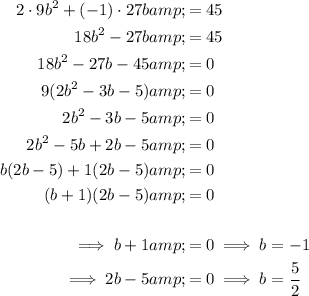
Therefore the possible values of the constant b are:

`b = -1, \quad b = (5)/(2)`