Question

Find the area of the shaded region. Use 3.14 for π as necessary.The circle centered on point A, and has a radius of 4 cm, is shaded. BC is a diameter of the circle. Point D is on the cicle, such that line AD is perpendicular to line BC. Triangle BCD is not shaded.A. 18.2 cm²B. 34.2 cm²C. 28.5 cm²D. 17.1 cm²

Answer 1

Given the circle centered on point A, you can identify that the triangle BCD is inside the circle.

You can identify that the shaded region can be obtained by subtracting the area of the triangle from the area of the circle.

The formula for calculating the area of a circle is:

`A_(circle)=\pi r^2`

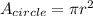
Where "r" is the radius of the circle.

In this case:

`r=4\text{ }cm`

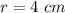
The formula for calculating the area of a triangle is:

`A_(triangle)=(bh)/(2)`

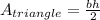
Where "b" is the base and "h" is the height.

In this case, you can identify that the base of the triangle is twice the radius of the circle (its diameter). Then:

`\begin{gathered} b=4\text{ }cm\cdot2=8\text{ }cm \\ h=4\text{ }cm \end{gathered}`

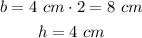
Therefore, you can set up that:

`A_(shaded)=\pi r^2-(bh)/(2)`

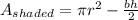
You must use:

`\pi\approx3.14`

Then, by substituting values into the equation and evaluating, you get:

`A_(shaded)=(3.14)(4\text{ }cm)^2-\frac{(8\text{ }cm)(4\text{ }cm)}{2}`
`A_(shaded)\approx34.2\text{ }cm^2`

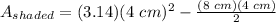
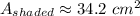
Hence, the answer is: Option B.