Question

two objects attract each other with a gravitational force of 18 units. the mass of one of the objects was tripled, and the distance between the objects tripled, what would be the new gravitational force of attraction between the two objects?

Answer 1

6 units

Step-by-step explanation:

Gravitational force between two objects is given by the equation

`F = G (m_1m_2)/(r^2)`

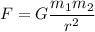
where

`G =`universal gravitational constant

`m_1`,
`;m_2` are the masses of the objects

`r` = distance between the objects

We are given that F = 18 units.

If m₁ is tripled and r is also tripled then

new F = F':

`F' = G (3m_1 \cdot m_2)/((3r)^2)\\\\\\F' = G (3m_1 \cdot m_2)/(9r^(2))\\\\\\So (F')/(F) = G (3m_1 \cdot m_2)/(9r^(2)) / G (m_1 \cdot m_2)/(r^(2))`

`= (3)/(9) = (1)/(3)\\`

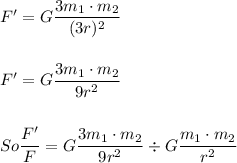
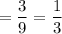
Therefore the new F is 1/3 of the old f

In this case that would be 18/3 = 6 units