Question

Endpoints of a diameter are (−5,−11) and (−1,1) Find the standard form of the equation for the circle with the following properties.

Answer 1

Standard form of the equation for the circle

(x + 3)² + (y + 5)² = 40

Explanation:

The equation of a circle in standard form is

`\boxed{(x - a)^2 + (y-b)^2= r^2}`

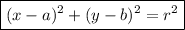
where (a, b) is the center of the circle and r is the radius

To find center of circle

The end points of the diameter are (-5, -11) and (-1, 1)

The center of the circle is midway between these two points

The x-coordinate of the midpoint = (-5 + -1)/2 = -6/2 = -3

The y-coordinate of the midpoint is (-11 + 1) /2 = -10/2 = -5

So the center of the circle is at (-3, -5)

To find the radius,

Calculate the distance from (-3, -5) to any of of the endpoints.

Let's take the endpoint (-1, 1) and find its distance from (-3, -5)

The distance between any two points (x₁, y₁) and (x₂, y₂) is calculated from the formula

`d^2 = {(x_(2) - x_(1))^2 + (y_(2) - y_(1))^2`

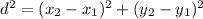
Substituting
(x₁, y₁) = (-1, 1)
(x₂, y₂) = (-3, -5)

and r for distance

we get

`r^2 = {(-3 - (-1))^2 + (-5 - 1)^2`

`r^2 = {(-2)^2 + (-6)^2}`

`r^2 = {{4} + {36}}`

`r^2 = {40}`

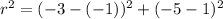
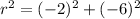
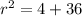
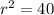
So the center (a, b) is (-3, -5) and r² =40

Plugging this into the circle equation:
(x - (-3))² + (y - (-5))² = 40

(x + 3)² + (y + 5)² = 40