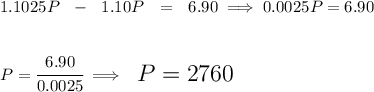Question

1 The difference between the simple interest and compound interest on a sum put out for 2 years at 5% was 6.90 .find the sum​

Answer 1

so we're assuming the compounding period is annual, so hmmm let's call our sum "P", how much is it at simple and compound interest anyway?

`~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\\ r=rate\to 5\%\to (5)/(100)\dotfill &0.05\\ t=years\dotfill &2 \end{cases} \\\\\\ A = P[1+(0.05)(2)] \implies \boxed{A = 1.10P} \\\\[-0.35em] ~\dotfill`

`~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\\ r=rate\to 5\%\to (5)/(100)\dotfill &0.05\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{annual, thus once} \end{array}\dotfill &1\\ t=years\dotfill &2 \end{cases} \\\\\\ A = P\left(1+(0.05)/(1)\right)^(1\cdot 2) \implies \boxed{A = 1.1025P}`

now, the larger one will be the compound interest one, so, let's subtract the simple interest one from it to get 6.90

`1.1025P~~ - ~~1.10P~~ = ~~6.90\implies 0.0025P=6.90 \\\\\\ P=\cfrac{6.90}{0.0025}\implies {\Large \begin{array}{llll} P=2760 \end{array}}`