Question

Use the rational zeros test to find all rational zeros of f(x)=x^3-4x^2+x+6

Answer 1

Zeros: -1, 2, and 3

Step-by-step explanation

The rational zeros theorem states that if a polynomial has integer coefficients, then any rational zero is in the form,

`(p)/(q)`

Where p is a factor of the last term of the polynomial, and q is a factor of the leading coefficient. If we have the polynomial,

`f(x)=a_nx^n+a_(n-1)x^(n-1)+...+a_1x+a_0`

Then the rational zeros are in the form,

`(p)/(q)=\frac{a\text{ }factor\text{ }of\text{ }a_0}{a\text{ }factor\text{ }of\text{ }a_n}`

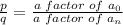
In this case, we have the polynomial,

`f(x)=x^3-4x^2+x+6`

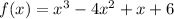
The first term is 1, so its factors are 1 and -1, while the last term is 6 and its factors are ±1, ±2, ±3, and ±6, so all the possible zeros are,

`\pm1,\pm2,\pm3,\pm6`

Let's try to divide the polynomial by (x + 1). If the remainder is 0, then -1 is a factor,

So, the factored polynomial is,

`f(x)=(x+1)(x^2-5x+6)`

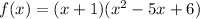
Now, for the second factor, we use the same theorem. Note that the first and last coefficients are the same as the original polynomial, so the list of possible zeros is the same,

`\pm1,\pm2,\pm3,\pm6`

Let's try with +2. Divide the 2nd-degree polynomial by (x - 2) and, if the remainder is 0, then +2 is a zero,

Thus, the factored polynomial is,

`f(x)=(x+1)(x-2)(x-3)`

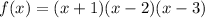
And, therefore, the zeros are -1, 2, and 3.