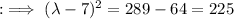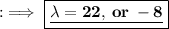Let's first understand what's relative here, it refers to Point of reference , the point, in respect to which other's position are to be considered, which here is O, the Origin with coordinates (0,0) as we are talking about two-dimensional reference frame. What position vector means? Say, we have the point of Reference X, and we've the position vector of Y with respect to X, then it can be written as
 . Now, using this simple rule we can have,
. Now, using this simple rule we can have,
Now, let's calculate
 firstly;
firstly;
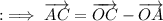

Now, here
 just means the the magnitude of the vector [tex{\overrightarow{AC}}[/tex], and we're aware that magnitude of a vector
just means the the magnitude of the vector [tex{\overrightarow{AC}}[/tex], and we're aware that magnitude of a vector
 is given by,
is given by,
 , so according to question;
, so according to question;

Squaring both sides;