Question

What is the y-intercept of y = x^2 - 3x + 2 by completed square form?

Answer 1

y-intercept(s): (0,−2)

Answer 2

2

Explanation:

The
`x^(2)` and x terms are made to follow the sequence:

`[a-b]^(2) =a^(2) -2ab + b^(2)`

Therefore the
`b^(2)` term has to be added to complete the
`[a -b]^(2)` sequence, but at the same time the
`b^(2)` term has to be balanced as it is not originally present in the equation:

`y = x^(2) - 3x + 2 = [(x)^(2) - 2(x)((3)/(2)) + ((3)/(2))^(2)] + 2 - ((3)/(2))^(2)`

`= [x - (3)/(2)]^(2) + 2 - (9)/(4)`

=
`[x - (3)/(2)]^(2) + (8)/(4) - (9)/(4)`

=
`[x- (3)/(2)]^(2) (+ 8-9)/(4)`

=
`[x-(3)/(2)]^(2) -(1)/(4)`

y-intercept is the y-value obtained when x = 0 in the equation:

`= [0 - (3)/(2)]^(2) -(1)/(4)`

=
`(-(3)/(2))^(2) -(1)/(4)`

=
`(9)/(4) - (1)/(4)`

=
`(8)/(4)`

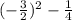
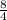
= 2