Question

The length of each side of an equilateral triangle having an area of square root of 243sq.cm is​

Answer 1

`\textrm{Each side = 23.6893 cm}\\\\\\\textrm{Rounded to 2 decimal places = 23.69 cm}\\\\\textrm{Rounded to 1 decimal place = 23.7 cm}`

You can choose the level of precision as desired from the above

Explanation:

The area of an equilateral triangle of side a

is

`A = ((a^2 √(3)))/(4)`

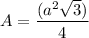
We are given A = 243

Plugging in values we get

`243 = (a^2√(3))/(4)`

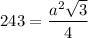
Switch sides so
`a^2` term is on the left

`(a^2√(3))/(4) = 243`

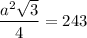
Multiply by 4 both sides to get rid of the denominator:

`(a^2√(3))/(4) * 4 = 243 * 4\\\\a^2√(3) = 972\\\\`

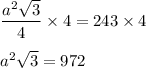
Divide by
`√(3)` both sides:

`a^2 = (972)/(√(3))\\\\a^2 = 561.18446\\\\a = \pm √(561.18446)\\\\`

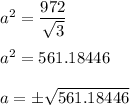
Taking only positive square root:

`a = √(561.18446)\\\\a = 23.6893\\\\`