Question

Please work these out, If possible can someone just work out 1 providing solutions. Thanks ​

Answer 1

See below for solution steps for parts (a) and (c)

Explanation:

The trick here is to get all the roots to have the same radical. Each of the lowest radical is the square root pf a prime so cannot be reduced further

For example, in a, the lowest is
`√(3)`

So get all the others to this level a
`√(3)` and then you can just add up the non-radicals and use the radical as the common expression

I will solve a couple and that will give you a general idea of solving the rest

Let's do a.

`5√(3) , √(3)` are already at the lowest radical level of
`√(3)` so let's reduce 108 to have
`√(108)` to have
`√(3)` as one of its components

We can factor 108 as follows;

108/3 = 36

So 108 = 36 x 3

√108 = √36 × √3 = 6√3

Therefore the original expression becomes

`5√(3) - 6√(3) + √(3) = (5 - 6 + 1)√(3) = 0 √(3) = 0`

`-------------------------------`

c.

`2√(20) - 7√(5) + √(45)`

Lowest radical is
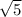`√(5)` whose coefficient is 7

Factor 20 = 4 x 5

`2√(20) = 2√(4 * 5) = 2√(4) * √(5) = 2* 2 * √(5)\\= \bold{4√(5)}`

Factor 45:
45 = 9 x 5

`√(45) = √(9) * √(5) = \bold{3√(5)}`

Original expression becomes:

`4√(5) - 7√(5) + 3√(5)\\\\=(4 - 7 + 3)√(5)\\\\= 0 √(5)\\\\= 0\\----------------------------`

I am sure you can do the rest. If not post them as another question. Maybe someone else will answer a few of the ones I did not.

All the best