Question

2. Determine the area of each composite figure below.

Answer 1

`6\pi`

Explanation:

There's two things to note here, we're dealing with a semi-circle and also a semi-circle that has some area taken out of it.

Area of a Circle:

The area of a circle can be calculated using the formula:
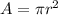`A=\pi r^2` where "r" is the radius, equal to half the diameter.

Since we're dealing with the semi-circles, we can just divide this area by two to get:
`A=(\pi r^2)/(2)`

Now as noted, we have some of the area taken out, but fortunately it's just another semi-circle. We can simply calculate the area of the entire semi-circle, and then calculate the area of the semi-circle inside and subtract them.

So the diameter of the entire thing is just 8 ft, so the radius is half of this, equal to 8 ft. That means the area is:
`A=(\pi (4)^2)/(2)=A = (\pi * 16)/(2) = 8\pi`

One mistake that may be made here, is assuming the radius of the smaller semi-circle is just two, as provided in the image. It's actually the radius of the inner semi-circle plus two which gives us the radius of the outer circle, of 4 feet. Now luckily in this case, it actually still results in 2 ft (since 2 + 2 = 4), but in other examples, that may noe be the case.

So now let's calculate the area of the inner semi-circle:
`A=(\pi (2)^2)/(2)=2\pi`

Now let's just subtract the areas:
`8\pi - 2\pi = 6\pi`, so the area is 6 pi