Answer:
(a) Possible number(s) of positive real zeros: 3
(b) Possible number(s) of negative real zeros: 1
Explanation:
Descartes' Rule of Signs tells us the maximum number of positive and negative roots.
Positive root case
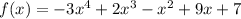
As there are 3 sign changes, the maximum possible number of positive roots is 3.
Negative root case
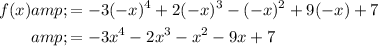
As there is one sign change, the maximum possible number of negative roots is 1.