Question

Select all of the following tables which could represent a linear function.059(a)5-15-35-5510155102025k(2)6163646f(x)-5051015153555h()5051015uno30105230

Answer 1

last table

Step-by-step explanation:

For a table to represent linear function, it must be in the form:

`\begin{gathered} y\text{ = mx + b} \\ m\text{ = slope, b = y-intercept} \end{gathered}`

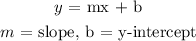
a) slope for this table using any two points: (0, 5) and (5, -15)

slope = (-15 - 5)/(5- 0) = -20/5

slope = -4

b is the value of y when x = 0

b = 5

`\begin{gathered} y\text{ }=\text{ -4x + 5} \\ \text{For each of the values of x we insert in the equation, we will get the value of y on the table.} \\ \\ \text{Hence, it is a linear function} \end{gathered}`

b) slope from (5, 6) and (10, 16)

slope = (16 - 6)/(10 - 5) = 10/5

slope = 2

There is no value of x = 0 on the table, we calculate for b using the point (5, 6)

y = mx + b

6 = 2(5) + b

b = -4

`\begin{gathered} \text{y = 2x - 6} \\ \text{For each of the values of x we insert in the equation, we will get the value of y on the table.} \\ \\ \text{Hence, it is a linear function} \end{gathered}`

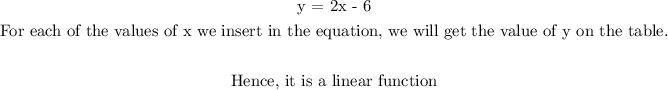
c) using point (0, -5) and (5, 15)

slope = (15 - (-5))/(5 - 0) = 20/5

slope = 4

when x = 0, y = -5

b = -5

`\begin{gathered} y\text{ = 4x - 5} \\ \text{For each of the values of x we insert in the equation, we will get the value of y on the table.} \\ \\ \text{Hence, it is a linear function} \end{gathered}`

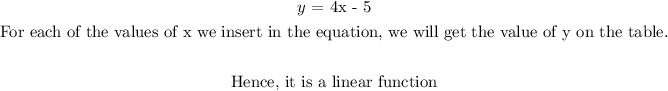
d) using point (0, 5) and (5, 30)

slope = (30 - 5)/(5 - 0) = 25/5

slope = 5

when x = 0 , y = 5

y -intercept = 5

`\begin{gathered} y\text{ = 5x + 5} \\ \text{when x = 5} \\ y\text{ = 5(5) + 5 = 30} \\ when\text{ x = 10} \\ y\text{ = 5(10) + 5 = 55} \\ \text{This is not the same y value in the table} \\ \text{when x = }15 \\ \text{y = 5(15) + 5 = 80} \\ \text{This is not the same y value in the table} \end{gathered}`

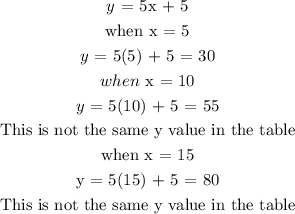
From the above, the last table is not a linear function