last table
Step-by-step explanation:
For a table to represent linear function, it must be in the form:
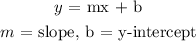
a) slope for this table using any two points: (0, 5) and (5, -15)
slope = (-15 - 5)/(5- 0) = -20/5
slope = -4
b is the value of y when x = 0
b = 5
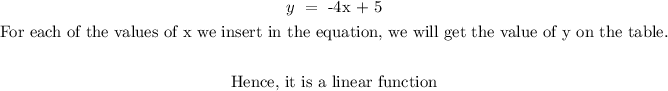
b) slope from (5, 6) and (10, 16)
slope = (16 - 6)/(10 - 5) = 10/5
slope = 2
There is no value of x = 0 on the table, we calculate for b using the point (5, 6)
y = mx + b
6 = 2(5) + b
b = -4
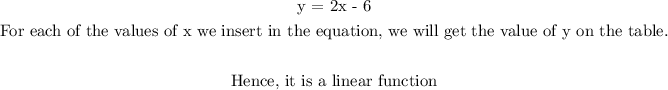
c) using point (0, -5) and (5, 15)
slope = (15 - (-5))/(5 - 0) = 20/5
slope = 4
when x = 0, y = -5
b = -5
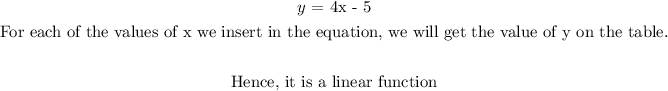
d) using point (0, 5) and (5, 30)
slope = (30 - 5)/(5 - 0) = 25/5
slope = 5
when x = 0 , y = 5
y -intercept = 5
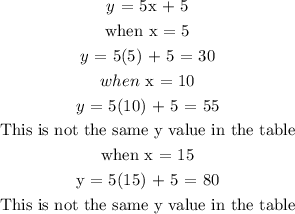
From the above, the last table is not a linear function