Answer:
![\mathbf{C_(Out) = C_o \ exp \Big [ - \Big ( (1)/((V)/(Q) ) + k \Big) t \Big ] }](https://img.qammunity.org/2022/formulas/chemistry/college/5k2etu4kt9s7m7v2suigqyq12rc8ejlzmf.png)
Step-by-step explanation:
The equation that describes the concentration of the radon in the basement with time Ct is;
![\mathbf{C_(Out) = C_o \ exp \Big [ - \Big ( (1)/(\theta) + k \Big) t \Big ] }](https://img.qammunity.org/2022/formulas/chemistry/college/4jh6va800osdnvl4tb3k7xybvl2hqtv88r.png)
where;
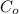 = concentration of the radon
= concentration of the radon
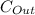 = allowable radon concentration
= allowable radon concentration
k = decay rate constant
= theoretical detention
t = time needed to lower the radon concentration
The theoretical detention

∴
![\mathbf{C_(Out) = C_o \ exp \Big [ - \Big ( (1)/((V)/(Q) ) + k \Big) t \Big ] }](https://img.qammunity.org/2022/formulas/chemistry/college/5k2etu4kt9s7m7v2suigqyq12rc8ejlzmf.png)