Question

Factorise (i) 4y²-6yz+9z²

Answer please ​

Answer 1

To factorize the expression
`\sf\:4y^2 - 6yz + 9z^2 \\`, we can use the quadratic formula.

We have the quadratic expression
`\sf\:ax^2 + bx + c \\`, where $$\sf\:a = 4$$, $$\sf\:b = -6y $$, and $$\sf\:c = 9z^2 $$.

The quadratic formula states that for any quadratic equation of the form
`\sf\:ax^2 + bx + c = 0 \\`, the solutions for $$\sf\:x $$ can be found using the formula:

`\sf\:x = (-b \pm √(b^2 - 4ac))/(2a) \\`

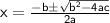
Applying this formula to our quadratic expression, we get:

`\begin{align}\sf\:x &= (-(-6y) \pm √((-6y)^2 - 4(4)(9z^2)))/(2(4)) \\ &= (6y \pm √(36y^2 - 144z^2))/(8) \\ &= (6y \pm √(36(y^2 - 4z^2)))/(8) \\ &= (6y \pm 6√(y^2 - 4z^2))/(8) \\ &= (3)/(4)y \pm (3)/(4)√(y^2 - 4z^2)\end{align} \\`

Thus, the factored form of the expression
`\sf\:4y^2 - 6yz + 9z^2 \\` is
`\sf\:((3)/(4)y + (3)/(4)√(y^2 - 4z^2))((3)/(4)y - (3)/(4)√(y^2 - 4z^2)) \\`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

✨
`\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`

Answer 2

`{ \qquad\qquad\huge\underline{{\sf Answer}}}`

The identity to be used here is [ (a - b)² = a² - 2ab + b² ]

First, try to get the given expression in form of terms on the RHS of the above identity

`\qquad \sf  \dashrightarrow \: 4y {}^(2) - 6yz + 9 {z}^(2)`

`\qquad \sf  \dashrightarrow \: (2 {}^(2))( {y}^(2)) - 2(3)(y)(z) + (3 {}^(2) ) {z}^(2)`

`\qquad \sf  \dashrightarrow \: (2y) {}^(2) - (2y)(3z) + (3z) {}^(2)`

[ it's in form of a² - ab + b² now, add and deduct ab here ]

`\qquad \sf  \dashrightarrow \: (2y) {}^(2) - (2y)(3z) + (9z) {}^(2) - (2y)(3z) + (2y)(3z)`

`\qquad \sf  \dashrightarrow \: (2y) {}^(2) - 2(2y)(3z) + (3z) {}^(2) + (2y)(3z)`

[ Apply the identity ]

`\qquad \sf  \dashrightarrow \: (2y - 3z) {}^(2) + (2y)(3z)`

`\qquad \sf  \dashrightarrow \: (2y - 3z) {}^(2) + 6yz`

[ That's probably the answer, it can't be simplified more ]