Given
Karen is painting the floor and four walls of a basement.
The basement is 12.0 m long, 4.0 m wide, and 2.5 m high.
Paint comes in 4 L cans.
One litre of paint covers 10 m.
To find:
a) What area does Karen need to paint?
b) How many cans of paint does Karen need?
Step-by-step explanation:
It s given that,
Karen is painting the floor and four walls of a basement.
The basement is 12.0 m long, 4.0 m wide, and 2.5 m high.
Paint comes in 4 L cans.
One litre of paint covers 10 m.
That implies,
a)
The area Karen needed to paint is,
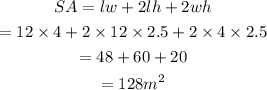
Hence, the area Karen needed to paint is 128m².
b) The number of cans of paint Karen needed is,
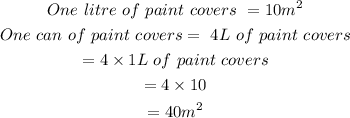
Therefore,
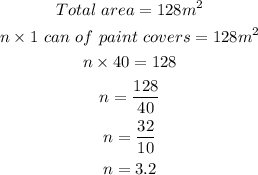
Hence, Karen needs a little more than 3 cans. So the answer is 4 Cans.