Question

. What is the rate of change of the area of a square with respect to its side length when

Answer 1

Given:

`A(s)=s^2`

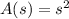
To get the rate of change of the area of a square with respect to its side, we differentiate the area with respect to the side.

Hence,

`\begin{gathered} A(s)=s^2 \\ (dA)/(ds)=2s \\ \\ \text{Hence, the rate of change is 2s} \end{gathered}`

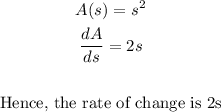
Hence, when s = 6, the rate of change is;

`\begin{gathered} (dA)/(ds)=2s=2*6 \\ (dA)/(ds)=12 \end{gathered}`

Therefore, the rate of change of the area of a square with respect to its side length when s=6 is 12.