Question

If pure water boils at 99.8 degrees celcius, what is the expected elevated boiling point of a solution of 2.50g of CaCl2, in 50.0mL (i.e., 50.0g) of H2O? For CaCl2, i = 3

Answer 1

INFORMATION:

We know that:

- pure water boils at 99.8 degrees celcius

And we must calculate the expected elevated boiling point of a solution of 2.50g of CaCl2, in 50.0mL (i.e., 50.0g) of H2O

STEP BY STEP EXPLANATION:

To calculate it, we need to use that:

Boiling point of solution = boiling point of pure solvent + boiling point elevation (ΔTb)

The elevation in boiling point (ΔTb) is proportional to the concentration of the solute in the solution. It can be calculated via the following equation.

`ΔTb=i* k_b* m`

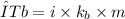
Where,

- i is the Van’t Hoff factor

- Kb is the ebullioscopic constant

- m is the molality of the solute

From given information, we know that:

- i = 3

Now, the ebullioscopic constant (Kb) is often expressed in terms of °C * kg * mol^-1. The value of Kb for water is 0.512.

So, kb = 0.512 °C * kg * mol^-1

Then, we must calculate the molality

`\begin{gathered} Molality=\frac{\text{ moles of solute}}{\text{ kg of solvent}} \\ Molality=((2.5g)/(110.98(g)/(mol)))/(0.05kg)=0.45(mol)/(kg) \end{gathered}`

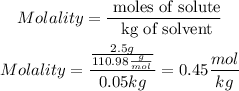
So, m = 0.45 mol/kg

Replacing the values in the formula for ΔTb

`\begin{gathered} ΔT_b=3*0.512(\degree C\cdot kg)/(mol)*0.45(mol)/(kg) \\ ΔT_b=0.69\degree C \end{gathered}`

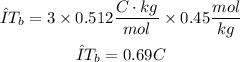
Finally, the expected elevated boiling point of the solution would be

`\text{ Boling point of solution}=99.8\degree C+0.69\degree C=100.49\degree C`

ANSWER:

The expected elevated boiling point of the solution is 100.49 °C