Question

Jenny swam 8 kilometers against the current in the same amount of time it took her to swim 16 kilometers with the current. The rate of the current was 1 kilometer per hour.

How fast would Jenny swim if there were no current?

Answer 1

`{ \qquad\qquad\huge\underline{{\sf Answer}}}`

Let the time taken by Jeeny in both the cases be " t " ~

Now, during upstream : current flow opposes the flow of swimmer (Jenny)

Let her actual speed without current be " v ", so her speed in current (upstream) will be :

`\qquad \sf  \dashrightarrow \: v - 1 \: \: kmph`

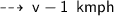
Now, according to formula :

`\qquad \sf  \dashrightarrow \: distance = speed * time`

`\qquad \sf  \dashrightarrow \: 8 = (v - 1)t \: \: \: \: \: - (1)`

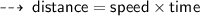
Next, durijg dowstream : current flow supporta the flow of swimmer (Jenny)

So, her speed while going downstream will be :

`\qquad \sf  \dashrightarrow \: v +1 \: \: kmph`

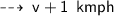
By same formula,

`\qquad \sf  \dashrightarrow \: 16 = (v + 1)t \: \: \: \: \: - (2)`

Now, solve the two equations ~

[ since time taken by her in both the cases is same, we use t in both equations ]

Divide equation (1) by equation (2) :

`\qquad \sf  \dashrightarrow \: (8)/(16) = (v - 1)/(v + 1)`

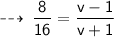
[ t gets canceled out ]

`\qquad \sf  \dashrightarrow \: (1)/(2) = (v - 1)/(v + 1)`

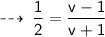
[ cross multiply ]

`\qquad \sf  \dashrightarrow \: v + 1 = 2(v - 1)`

`\qquad \sf  \dashrightarrow \: v + 1 = 2v - 2`

`\qquad \sf  \dashrightarrow \: 2v - v = 1 - ( - 2)`

`\qquad \sf  \dashrightarrow \: v = 1 + 2`

`\qquad \sf  \dashrightarrow \: v = 3 \: \: kmph`

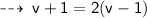
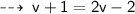
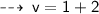
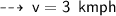
That's the required answer ~ [ Jimmy would swim at the rate of 3 kmph if she there was no current ]