Answer:
a) 0.677
b) 0.0431
c) 0
Explanation:
For each bit, there are only two possible outcomes. Either it is correctly received, or it is erroneously received. Whether any particular bit is erroneously received is independent of whether any other bit is erroneously received. This means that we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
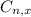 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
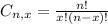
And p is the probability of X happening.
10% of all bits transmitted through a digital communication channel are erroneously
This means that
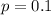
Messages of 20 bits:
This means that

a. What proportion of these messages will have at most 2 erroneously received bits?
This is
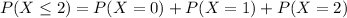 . So
. So

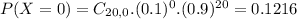
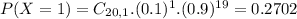
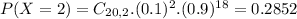
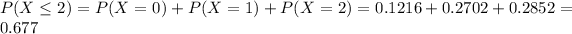
b. What proportion of these messages will have at least 5 erroneously received bits?
This is
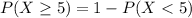
In which
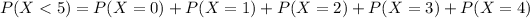 . So
. So

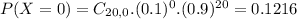
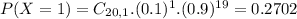
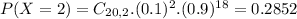
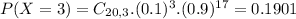
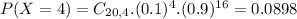
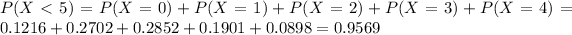
Then
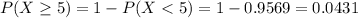
c. For what proportion of these messages will more than half the bits be erroneously received?
This is
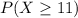
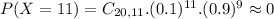
If 11 is approximately 0, the rest(11, 12, 13,...) will also be approximately 0. So this proportion is 0.