Answer:
Values of x are ±4 and ±5
Explanation:
Let y =

Which means:
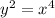
Therefore:
A quadratic equation is formed:
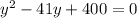
The above quadratic equation can be simplified either by The Double Bubble Method or using the quadratic formula
Double Bubble Method:
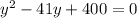
The pair of factors of 400 that add together to give 41 are 25 and 16. Use these two factors to rewritre -41y:
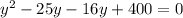
Then do Factorization by grouping (i.e group the terms with common factors before factorizing):
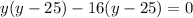

The product of two expressions is zero, which means either of the two expressions is equal to Zero:
Either:
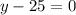
Substituting
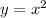 :
:
=
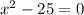
=
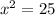
=
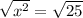
∴ x = ±5
Or:
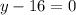
Substituting
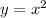
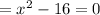
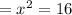

∴ x = ±4
∴Values of x are ±4 and ±5