Answer:
One daylily costs $9, and one pot of ivy costs $9.
Explanation:
Step 1: Write a System of Algebraic Equations
We are given 2 different variables, or "unknowns", that we need to find the value of here - the cost of one daylily, and the cost of one pot of ivy. We know that the cost of each plant remains constant (doesn't change), and we are given the following information:
- 1 daylily and 8 pots of ivy cost $81.
- 10 daylilies and 11 pots of ivy cost $189.
We can see that we have a system of equations in the making. The first thing to do when writing a system is assign letters to variables. Let's let the cost of one daylily be denoted as
, and the cost of one pot of ivy be denoted as
(in dollars for each). From the above information, we can write the system:
Step 2: Solve the System (with Substitution)
Now that we have a solution, let's use it to solve for the value of each variable. There are many ways to do this (addition, subtraction, etc), but it seems that the quickest way to solve this particular system is using the substitution method. This is where you write one variable in terms of the others by manipulating one equation, and then substituting that expression in for the isolated variable in the other equation. It's easy to do this here because we already have a
in (1).
Isolating
in (1) by subtracting
from both sides, we get:
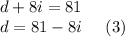
Substituting (3) into (2) and solving for i, we get:
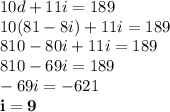
Substituting this value into (3), we get:
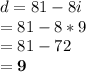
Therefore, one daylily costs $9, and one pot of ivy costs $9.