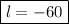A rectangle has a length of 30 feet less than five times its width if the area of the rectangle is 360 ft.² find the length of the rectangle

Question

asked Sep 26, 2024 163k views

1 Answer

Levi · Answer 1 · 2024-09-29T18:28:55+0000

Answer:

l = 30 OR
l=-60

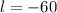
Explanation:

We can solve this problem with a system of equations by creating 2 equations from the information given.

1. "a length of 30 feet less than 5 times its width"

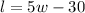
l = 5w - 30

2. "the area of the rectangle is 360 ft²"

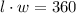
$l\cdot w = 360$

To solve for the rectangle's length, we can create a substitution for w by dividing both sides of the second equation by length (
).

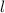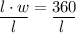
$l\cdot w = 360\\\overline{\ \ l\ \ } \ \ \ \: \ \overline{\ l \ \ }$

w = (360)/(l)

Then, we can substitute this value back into the first equation and solve for
.

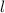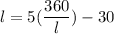
l = 5((360)/(l)) - 30

↓ distribute the 5

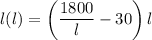
$l(l) = \left((1800)/(l) - 30\right)l$

↓ multiply both sides by

l^2 = 1800 - 30l

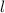
↓ move all
's to one side

l^2 + 30l = 1800

To solve this quadratic, we can complete the square.

↓ add (30/2)² to both sides

$l^2 + 30l + \left((30)/(2)\right)^2 = 1800 + 15^2$

↓ simplify 15²

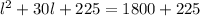
l^2 + 30l + 225 = 1800 + 225

↓ factor the left side as a perfect square

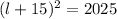
(l + 15)^2 = 2025

↓ take the square root of both sides

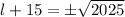
$l + 15 = \pm √(2025)$

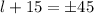
$l + 15 = \pm 45$

↓ split into 2 equations

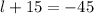
l + 15 = 45 OR
l + 15 = -45

$\boxed{l = 30}$ OR
$\boxed{l=-60}$