Question

Calculate the moment of inertia of a thin rim, with mass m = 10kg, and radius R = 20cm with respect to an axis perpendicular to its plane, which passes through a point on its circumference.

Answer 1

Given data

*The given mass of thin rim is m = 10 kg

*The given radius of the rim is r = 20 cm = 0.20 m

The formla for the moment of inertia of thin rim with respect to an axis perpendicular to its plane, which passes through a point on its circumference is given as

`\begin{gathered} I=mr^2+mr^2 \\ =2mr^2 \end{gathered}`

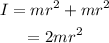
Substitute the known values in the above expression as

`\begin{gathered} I=2(10)(0.20)^2 \\ =0.8kg.m^2 \end{gathered}`

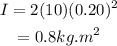
Hence, the moment of inertia of thin rim with respect to an axis perpendicular to its plane, which passes through a point on its circumference is I = 0.8 kg.m^2