Question

You are on a team of architects. You are charged with building a scale-model replica of one section of a new roller coaster before construction gets underway.

Certain reinforcement cables and struts are required to make the roller coaster sturdier. The goal for this project is for your team to determine where to place these cables or struts. The mathematical models for these reinforcements are known.


Your team must provide both algebraic and graphical evidence for your conclusions regarding the location of the cables.


Directions:


The shape of this particular section of the rollercoaster is a half of a circle. Center the circle at the origin and assume the highest point on this leg of the roller coaster is 30 feet above the ground.




1. Write the equation that models the height of the roller coaster.


The circle equation is x² + y² = r²




Start by writing the equation of the circle. (Recall that the general form of a circle with the center at the origin is x2 + y2 = r2. (10 points)


The roller coaster's leg is 30 feet above the ground, as stated.


⇒ r = 30


⇒x² + y² = 30²


⇒x² + y² = 900




Now solve this equation for y. Remember the roller coaster is above ground, so you are only interested in the positive root. (10 points)


Roller coaster height equation: - x2 + y2 = 900




As we know, x² + y² = 900




⇒y² = 900 - x²




⇒y = √900 - x²






2. Graph the model of the roller coaster using the graphing calculator. Take a screenshot of your graph and paste the image below, or sketch a graph by hand. (5 points)



Model 1: One plan to secure the roller coaster is to use a chain fastened to two beams equidistant from the axis of symmetry of the roller coaster, as shown in the graph below:



You need to determine where to place the beams so that the chains are fastened to the rollercoaster at a height of 25 feet.




3. Write the equation you would need to solve to find the horizontal distance each beam is from the origin. (10 points)


To find the horizontal distance, we use the equation: x = 30^2-25^2



4. Algebraically solve the equation you found in step 3. Round your answer to the nearest hundredth. (10 points)


The horizontal distance is 16.58 feet


How to determine the equation:


The height is given as: 25 feet.

The roller coaster's length is 30 feet.

Use h to represent horizontal distance.

Given that the roller coaster represents the hypotenuse side length, the following equation can be used to calculate h

In step 3, we have: 30^2-25^2

This gives

Take the roots of both sides to get our answer





5. Explain where to place the two beams. (10 points)


The beam should be placed 8 feet from the center.


The struts are y = √(x + 8) and y = √(x − 4).


The struts are 2 feet apart at the location of the beam: √(x + 8) − √(x − 4) = 2


Solving:


√(x + 8) = 2 + √(x − 4)


x + 8 = 4 + 4√(x − 4) + x − 4


8 = 4√(x − 4)


2 = √(x − 4)


x − 4 = 4


x = 8




Model 2: Another plan to secure the roller coaster involves using a cable and strut. Using the center of the half-circle as the origin, the concrete strut can be modeled by the equation and the mathematical model for the cable is. The cable and the strut will intersect.




6. Graph the cable and the strut on the model of the roller coaster using the graphing calculator. Take a screenshot of your graph and paste the image below, or sketch a graph by hand. (5 points)






7. Algebraically find the point where the cable and the strut intersect. Interpret your answer. (10 points)




root 2x+8=x-8


2x+8=x^2-16x+64


-x^2+18x-56=0


x^2-18x+56=0


x(x-4)-14(x-4)=0


(X-4)(x-14)=0


x=4 ,x=14


x=14




Model 3: Another plan to secure the roller coaster involves placing two concrete struts on either side of the center of the leg of the roller coaster to add reinforcement against southerly winds in the region. Again, using the center of the half-circle as the origin, the struts are modeled by the equations and. A vertical reinforcement beam will extend from one strut to the other when the two cables are 2 feet apart.




8. Graph the two struts on the model of the roller coaster. Take a screenshot of your graph and paste the image below, or sketch a graph by hand. (5 points)



Recall that a reinforcement beam will extend from one strut to the other when the two struts are 2 feet apart.




9. Algebraically determine the x -value of where the beam should be placed. (15 points)



10. Explain where to place the beam. (10 points)

Answer 1

Step 1: Equation for Roller Coaster Height.

The general form for the equation of a circle at the origin is:

`\boxed{\left\begin{array}{ccc}\text{\underline{Equation of a Circle (at origin):}}\\\\x^2+y^2=r^2\\\\\bullet \ \text{where 'r' is the radius of the circle}\end{array}\right}`

It is given that the height of the roller coaster is 30 feet. Thus, r = 30. Plug this into the equation above and solve for 'y.'

`\Longrightarrow x^2+y^2=(30)^2\\\\\\\\\Longrightarrow x^2+y^2=900\\\\\\\\\therefore \boxed{\boxed{y=√(900-x^2) }}`

Step 2: Graph of Roller Coaster Model.

Refer to the attached image(s).

Step 3: Equation for Horizontal Distance of Beams.

Going back to the equation we got in step (1), we can solve for the variable ‘x.’

`\Longrightarrow y=√(900-x^2)\\\\\\\\\therefore \boxed{\boxed{x=\pm√(900-y^2)}}`

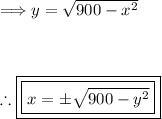
Step 4: Algebraic Solution for Beam Placement.

Given a height, y = 25 ft. We can plug this into the equation above and solve for 'x.'

`\Longrightarrow x=\pm√(900-(25)^2)\\\\\\\\\Longrightarrow x=\pm√(275)\\\\\\\\\Longrightarrow x=\pm5√(11)\\\\\\\\\therefore \boxed{\boxed{x\approx\pm16.58 \ ft}}`

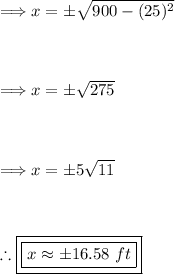
Step 5: Placement of Beams.

The beams should be placed 16.58 feet from either side of the origin.

Step 6: Graph of Cable and Strut.

Refer to the attached image(s).

Step 7: Algebraic Intersection of Cable and Strut.

To find the point of intersection, set the two given equations (from model 2) equal to each other and solve for 'x.'

`y=√(2x+8) \ \text{and} \ y=x-8\\ \\\\\\\Longrightarrow √(2x+8)=x-8 \\\\\\\\\Longrightarrow 2x+8=(x-8)^2 \\\\\\\\\Longrightarrow 2x+8=x^2-16x+64\\\\\\\\\Longrightarrow x^2-18x+56=0\\\\\\\\\Longrightarrow (x-14)(x-4)=0\\\\\\\\\therefore x=\{14,-4\}`

In order to determine which value of 'x' is correct we must verify the solution.

When x = 14:

`\Longrightarrow 2(14)+8=(14-8)^2\\\\\\\\\Longrightarrow 36=36 \checkmark`

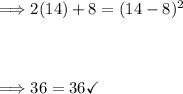
When x = -4:

`\Longrightarrow 2(-4)+8=(-4-8)^2\\\\\\\\\Longrightarrow 0\\eq 144`

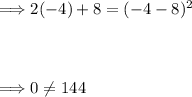
Thus, the correct x-value is 14. Plug this into either given equations and solve for 'y.'

`\Longrightarrow y =x-8\\\\\\\\\Longrightarrow y =14-8\\\\\\\\\therefore y=6`

Thus, the point of intersection is (14, 6).

Step 8: Graph of Two Struts.

Refer to the attached image(s).

Step 9: Algebraic Solution for Beam Placement.

To find the x-value of the beam placement, you need to find the point where the two strut equations are 2 feet apart. Set up an equation using the given functions and solve for 'x.'

`\Longrightarrow y=√(x+8)-√(x-4); \ y=2\\\\\\\\\Longrightarrow 2=√(x+8)-√(x-4)\\\\\\\\\Longrightarrow 2+√(x-4)=√(x+8)\\\\\\\\\Longrightarrow 4√(x-4)+x=x+8\\\\\\\\\Longrightarrow 4√(x-4)=8\\\\\\\\\Longrightarrow √(x-4)=2\\\\\\\\\Longrightarrow x-4=4\\\\\\\\\therefore \boxed{\boxed{x=8}}`

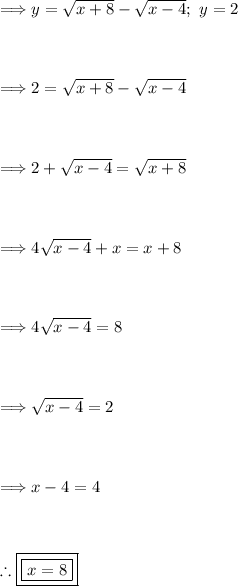
Step 10: Placement of Beam.

The beams will need to be placed 8 feet from either side of the origin.