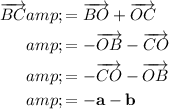Question

ABCD is a parallelogram.

The diagonals of ABCD intersect at O.
OA = a and OB = b
a) Express the vector CA in terms of a.
b) Express the vector AB in terms of a and b.
c) Express the vector BC in terms of a and b.

Answer 1

`\textsf{a)} \quad \overrightarrow{CA} =2\textbf{a}`

`\textsf{b)} \quad \overrightarrow{AB} =\textbf{b}-\textbf{a}`

`\textsf{c)} \quad \overrightarrow{BC} =-\textbf{a}-\textbf{b}`

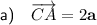
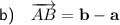
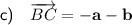
Explanation:

A parallelogram is a quadrilateral where opposite sides are equal in length and parallel to each other.

The diagonals of a parallelogram are not equal in length, but they bisect each other (divide into two equal parts).

Therefore, if OA = a then CO = a.

Similarly, if OB = b then DO = b.

Part (a)

Express the vector CA in terms of a:

`\begin{aligned}\overrightarrow{CA} &= \overrightarrow{CO} + \overrightarrow{OA}\\&=\textbf{a}+\textbf{a}\\&=2\textbf{a}\end{aligned}`

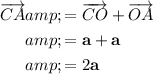
Part (b)

Express the vector AB in terms of a and b:

`\begin{aligned}\overrightarrow{AB} &= \overrightarrow{AO} + \overrightarrow{OB}\\&= -\overrightarrow{OA} + \overrightarrow{OB}\\&= \overrightarrow{OB}-\overrightarrow{OA}\\&=\textbf{b}-\textbf{a}\end{aligned}`

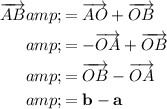
Part (c)

Express the vector BC in terms of a and b:

`\begin{aligned}\overrightarrow{BC} &= \overrightarrow{BO} + \overrightarrow{OC}\\&= -\overrightarrow{OB} - \overrightarrow{CO}\\&= -\overrightarrow{CO}-\overrightarrow{OB}\\&=-\textbf{a}-\textbf{b}\end{aligned}`