Given::
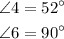
First, we find:
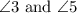
Since, the vertically opposite angles are equal.
Therefore,
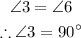
Next to find the angle of 5:
We have,
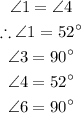
Since the angle of 2 and 5 are vertical angles and we know that the central angle is 360.
So that,
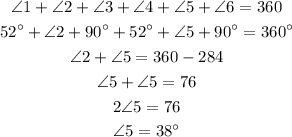
Hence, the measures of angle of 3 and 5 are,

Finally, to find the complementary pair of angle 1.
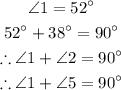
Hence, the two angles which are complementary to the angle of 1 is,
