Question

I know that the first term of the sequence is -2, and the fifth term is -1/8. What do you know?Type of sequence : Common ratio or difference : Explicit equation : Recursive equation :

Answer 1

Type of sequence: Geometric

Common ratio:
`\mbox{\large (1)/(2)}`

Explicit equation:

`a_n = a_1 \cdot \left((1)/(2)\right)^(n-1 )`

Recursive Equation:

`\mbox{\large a_n = (1)/(2) \cdot a_(n-1)}`

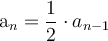
Explanation:

Looking at the first and fifth terms it appears to be a geometric sequence where each successive term is r x previous term

r is referred to as the common ratio = aₙ/aₙ₋₁ where aₙ is the nth term and aₙ₋₁ the previous term

The nth term can be found by using the formula
aₙ = a₁ x rⁿ⁻¹

where a₁ is the first term

We have a₁ = -2

a₅ = - 1/8

Plugging these into the general equation for a geometric sequence we get

`-(1)/(8) = -2 \cdot r^(5-1)\\\\\\-(1)/(8) = -2 \cdot r^(4)\\\\r^4 = -(1)/(8) / -2\\\\\\r^4 = (1)/(16)\\\\\\r = \sqrt[4]{(1)/(16)} \\\\r = (1)/(2) \;\;\;\;\textrm(since \; 2^4 = 16)`

Recursive equation relates the nth term to the (n-1)th term and is

`a_n = (1)/(2) \cdot a_(n-1)`

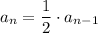
If we start at the first term

a₁ = -2

a₂ = 1/2 x (-2) = - 1

a₃ = 1/2 x (-1) = - 1/2

a₄ = 1/2 x (-1/2) = -1/4

a₅ = 1/2 x (-1/4) = - 1/8

So everything pans out fine