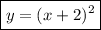Answer:
3.
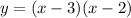
4.
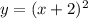
Explanation:
In this problem, we are asked to find the equations in their factored form of the graphed parabolas.
3. We can see that the parabola's vertex is at (3, -4). We can plug the coordinates of that point into the vertex form equation:

where
 is the vertex of the parabola.
is the vertex of the parabola.
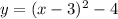
Then, we can expand the right side of the equation to an unfactored form.


Finally, we can factor the right side of the equation.
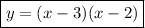
4. First, input the vertex's coordinates into the vertex form equation.
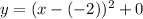
Then, simplify.
(Remember that subtracting a negative is the same as adding the positive)