Answer: 14 inches by 12 inches
Work Shown:
x = length
x-2 = width
area = length*width
area = x(x-2)
x(x-2) = 168
x^2-2x = 168
x^2-2x-168 = 0
Plug a = 1, b = -2, c = -168 into the quadratic formula.
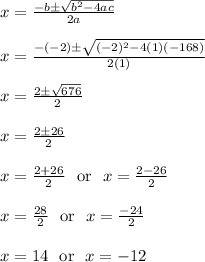
Ignore x = -12 since we cannot have a negative length.
The only practical solution is x = 14.
If x = 14, then x-2 = 14-2 = 12
The rectangular mirror is 14 inches by 12 inches
Check: area = length*width = 14*12 = 168
The answers are confirmed.